This article refers to the address: http://
0 PrefaceIn recent years, due to the great progress in the research of neural networks, the speed identification method based on BP neural network model has been widely studied, but it still has problems such as slow convergence speed and easy to fall into local minimum values. Therefore, for neural networks Optimization has always been a hot topic of current research. In this paper, chaos is introduced into Ant Colony Optimization (ACO) to form Chaos Ant Colony Optimization (CACO), which improves the optimization efficiency and accuracy of BP neural network and solves the above problems. At the same time, in the simulation test of the asynchronous motor direct torque control (DTC) speed identification, the accurate identification of the motor speed is realized.
1 shortcomings of BP neural network
BP neural network is a kind of neural network model widely used in the field of control. Its learning process consists of information forward calculation and error back propagation process. It uses a gradient search technique to minimize the mean squared error of the actual output value of the network and the desired output value. In addition, the network has good nonlinear mapping and generalization capabilities. The structure of the BP neural network is shown in Figure 1.

The mathematical model of BP neural network is:
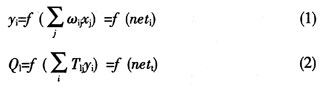
Where x j is the output of the input layer node, y i is the output of the hidden layer node, and O 1 is the output of the output layer. The network connection weight between the input layer node and the hidden layer node is ω ij ; the network connection weight between the hidden layer node and the output layer node is T li ; and the expected output of the output layer node l is t 1 . f(net) is the transfer function. To this end, the adjustment formula for its network connection weight is as follows:
Where η is the learning rate (η>0); k is the number of training times, and α is the smoothing factor (0<α<1), which is the hidden layer node error.
2 BP neural network chaotic ant colony optimization process
2.1 Basic Ant Colony Algorithm
The basic idea of ​​ACO is: at the initial moment of the algorithm, a certain number of ants are randomly placed in a given N cities, and the pheromone on each path is equal. During the movement, the ants independently select the next city according to the amount of pheromone on each path. The transfer rule used by the ant system is based on the probability of the ant's transition between the two cities. After completing a loop, the ant releases a certain amount of pheromone on the path. The path taken to complete a loop is a solution to the problem. When all the ants have completed the loop, the optimal solution is obtained.
The basic formula of the ant colony algorithm is as follows:

2.2 Chaos ant colony algorithm
The Chaos Ant Colony Algorithm (CACO) is inspired by the chaotic characteristics of natural ants walking and the self-organization characteristics of the entire population. It uses chaotic ergodicity and randomness to introduce the chaotic perturbation operator into the ant colony algorithm, and linearly maps the initialization variables with chaotic features to the variable value interval. The method takes into account the characteristics of chaotic dynamic search and intelligent search, which can effectively avoid the local optimization in the search process, thus improving the speed of the algorithm and the ability of global optimization.
(1) Chaos initialization
Let Ï„ ij (t) be the information concentration on the path at time t, and use the ergodicity of chaotic motion to initialize the chaos. The chaotic variable selection typical chaotic system Logistic mapping iteration formula is as follows:
In the formula, μ is the control parameter. When μ=4, Logistic is completely chaotic, and the system has ergodicity between [0, 1]. If the permutation variable is used to correspond to a path by using the permutation theory, that is, the pheromone concentration on each road segment is given an initial value τ ij (0) according to the amount of chaos, the convergence speed of the basic ant colony algorithm can be effectively solved. Slow question.
(2) Introducing chaotic disturbance
In the ant colony algorithm, if the ant later moves from point i to a point j, the pheromone Ï„ ij (t) is left on the path ij. After ant k completes any path, the pheromone on the path will be updated according to equation (5). It can be seen that this update method is easy to fall into the local optimal solution while speeding up the optimization. Therefore, the amount of chaotic perturbation is introduced here to adjust the pheromone so as to avoid falling into the local optimal extremum interval. The improved formula is:
Among them, X ij is the chaotic perturbation, which can be obtained by Logistic mapping of typical chaotic system, and q is the correlation coefficient.
2.3 Implementation steps of chaotic ant colony algorithm
The specific steps to implement the chaotic ant colony algorithm are as follows:
Step1: Initialize the BP network structure, and set the number of neurons in the input layer, hidden layer, and output layer of the network;
Step2: chaotic initialization pheromone concentration, individual optimal and global optimal;
Step3: Calculate the transition probability of each ant using formula (4);
Step4: According to the transition probability of each ant, the optimal path is obtained and the optimal value is compared. If it is better, the optimal value is updated;
Step 5: Compare the optimal value of each ant with the optimal value of the entire ant colony. If it is better, it will become the new optimal value of the whole ant colony;
Step6: Update and modify the pheromone concentration on the path ij according to formula (9);
Step7: Whether the comparison times reach the preset precision. If the preset precision is met, the weight and threshold of each dimension in the global optimal value of the last iteration is the requested; otherwise, returning to step3, the algorithm continues to iterate until it is satisfied. The conditions are up.
3 DTC-based system simulation
3.1 Direct Torque Control System Structure
The structural principle of the direct torque control (DTC) system is shown in Figure 2. In the α-β coordinate system, by obtaining the stator voltages U s α , U s β , the stator currents I s α , I s β and the stator current derivatives pI s α , pI s β normalized, the neural network can be constructed. The six inputs, after denormalization, can obtain the rotor speed ω, thus constructing a dynamic speed estimator.
3.2 Simulation experiment
When the simulation platform of the direct torque control system is established in the MATLAB/Simulink simulation environment, the system sampling period can be set to 0.1 ms. The other parameters of the asynchronous induction motor are: rated power P N =15 kW, rated voltage V N = 380 V, rated frequency f N =50 Hz, stator resistance R s =0.435 Ω, rotor resistance R r =0.816 Ω, stator inductance L s =0.002H, rotor inductance L r =0.002H, stator and rotor mutual inductance L m =0.06931 H, the pole pair p=2, the moment of inertia J=0.0918 kg.m 2 . When the motor speed is set to ω=20 rad/s, 1000 sets of data are taken as training samples, 5000 sets of data are used as verification samples, the maximum number of training times is set to 2000 times, and the minimum allowable error is set to 0.001.
The number of hidden layer nodes of the learning network is determined to be k 1 =11 and k 2 =6 after multiple trainings, and n is the number of input nodes. The number m of chaotic variables is the sum of the neural network ownership value and the threshold value, m=156, the ant colony population number M=30, p=0.8, Q=50. The algorithm training error comparison is listed in Table 1.
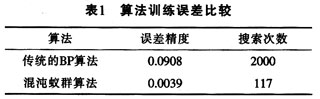
It can be seen from Table 1 that the minimum fitness of the traditional BP algorithm optimization neural network converges very slowly, and the error is large. The chaotic ant colony algorithm optimizes the BP neural network with smaller error and higher precision, and its convergence is far superior to the traditional BP algorithm.
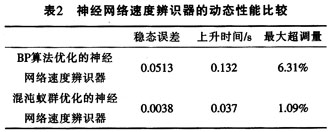
Table 2 lists the dynamic performance indicators of the neural network speed recognizer extracted from the experimental simulation results. It can be seen that the neural network optimized by chaotic ant colony has greatly improved compared with the dynamic performance of the traditional BP algorithm.
4 Conclusion
In this paper, a BP neural network model based on chaotic ant colony algorithm is constructed and applied to the speed recognizer in the direct torque control system, which shows the superior performance of its identification nonlinear function and its high speed and high precision. specialty. The simulation results show that the BP neural network velocity identifier optimized by chaotic ant colony is feasible, and has strong speed tracking accuracy. It can realize speed sensorless control of direct torque control system, and the system has good dynamic and static. performance.
WS2811 digital led strip is single signal transmission Led, the same as WS2812B and SK6812 with three-channel circuit,
But It is difference,the WS2811 IC can be inside or outside. and the working Voltage is DC5-24V, can be program and apply to all kinds of electronic products, electrical equipment running horse lamp, led pixel screen etc.
It is the most common product and demand on the market.
Waterproof Strip,WS2811 RGB LED Strip,WS2811 LED Strip,WS2811 Digital LED Strip
SHEN ZHEN SEL LIGHTING CO.,LTD , http://www.sellighting.com